2434 - Courbe de Jordan et Calcul de Carathéodory
N. Lygeros
Pour comprendre le contexte de l’article de C. Carathéodory intitulé : Exemples particuliers et théorie générale dans le calcul des variations, il est nécessaire de mettre en exergue différents travaux profonds d’analyse. En effet, comme le dirait M. Mizony, chacune de ses remarques cache une somme de difficultés techniques. L’une d’entre elles est la notion de courbe de Jordan. Et celle-ci implique aussi des difficultés d’ordre topologique.
Une courbe de Jordan est une courbe fermée simple dans le plan. En d’autres termes il s’agit d’une application continue et injective d’un cercle vers un plan. Sous cet aspect élémentaire se cache toute la problématique de la dérivation. Pour le constater il suffit de considérer le théorème de Jordan.
Théorème : Le complémentaire de l’image d’une courbe de Jordan dans le plan est formé de deux composantes connexes, dont l’une est bornée et l’autre non. Toutes deux ont pour frontière l’image de la courbe de Jordan.
B. Bolzano et C. Jordan ont tenté de démontrer ce théorème simple en apparence mais en apparence seulement. Mais ce n’est qu’en 1905 qu’O. Veblen l’a démontré. Et nous devons remarquer que le théorème de Jordan-Schönflies qui précise la topologie des composantes ne se généralise pas en dimension trois en raison du contre-exemple de la sphère à cornes de J. Alexander.
De manière plus concrète, pour comprendre la difficulté du théorème de Jordan il suffit de remarquer que le flocon de Von Koch est aussi une courbe de Jordan i.e. celle-ci peut être une courbe non différentiable en aucun de ses points. Aussi en termes plus modernes, à la suite des travaux de B. Mandelbrot, nous pouvons qualifier sa nature de fractale. Aussi en étudiant le calcul de C. Carathéodory sur la recherche d’une courbe joignant deux points fixes donnés pour laquelle une certaine intégrale curviligne atteint sa valeur minimum, il est nécessaire de garder toutes ces informations à l’esprit. Il considère la représentation conforme des deux plans (x,y) et (ξ,η) l’un sur l’autre donnée par la formule 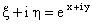 . Ainsi à chaque courbe x (t), y (t) du premier correspond une courbe ξ (t), η (t) du second. Comme
. Ainsi à chaque courbe x (t), y (t) du premier correspond une courbe ξ (t), η (t) du second. Comme 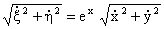 , l’intégrale curviligne à rendre minimum est donnée par la formule
, l’intégrale curviligne à rendre minimum est donnée par la formule
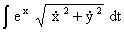 .
.Mais le point ξ = η = 0 n’est l’image d’aucun point situé à distance fixe dans le plan des (x,y). Cet exemple permet à C. Carathéodory de mettre en évidence une difficulté non découverte par Riemann d’une part et de montrer l’efficacité de la méthode d’Euler d’autre part.
Pour cela, il greffe, selon ses propres termes, une seconde transformation biunivoque du plan des (x,y) en lui-même, sur la représentation conforme du problème sous forme ordinaire. Et en modifiant sa méthode initiale, il aboutit aux relations suivantes :
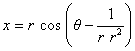 et
et 
et la fonction 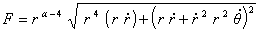
qui lui donne une métrique de Riemann, pour laquelle aucune ligne rectifiable joignant certains points du plan ne peut être une géodésique du problème. Cependant C. Carathéodory précise qu’il existe des courbes de Jordan qui répondent à la question.
