973 - Cryptographie et hypergroupes
N. Lygeros
Historiquement la cryptographie utilise l’efficacité de la théorie des groupes avant que celle-ci ne soit véritablement créée par Evariste Galois. Une des preuves les plus frappantes de cette affirmation, c’est le chiffre de Blaise de Vigenère. Celui-ci date de 1500 alors qu’il faudra attendre près de trois siècles avant l’invention de la notion de groupe. Pourtant le chiffre de Vigenère est basé sur la table de Vigenère qui est un cas particulier d’une table de Cayley, puisqu’elle est isomorphe au groupe additif des résidus modulo 26. Ce code qui a été introduit pour éviter l’obstacle de la distribution statistique immédiate, exploite les permutations de l’alphabet à 26 lettres comme nous pouvons le constater sur l’exemple suivant :
Exemple :

Nous avons donc une structure algébrique du type (G,.) et une équation ab=c qui a une unique solution pour permettre de retrouver le texte initial. Et c’est en cela que nous exploitons la structure de groupe. Cependant si nous regardons avec précision ce qui est nécessaire dans cette procédure, il est facile de nous rendre compte qu’un groupe n’est pas obligatoire, un hypergroupe est suffisant pour donner le rôle de codant. De plus en rendant plus complexe le codage, nous évitons qu’il soit directement percé par la méthode employée par Friedrich Kasisky dans le cas simple et par Charles Babage dans le cas complexe. Car cette fois, la clef contient deux secrets : premièrement l’alphabet et deuxièmement la longueur du code.
Exemple :
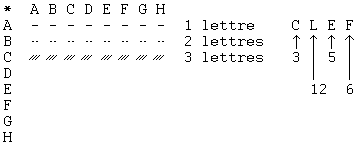
Ainsi le codage s’effectue en utilisant à tour de rôle les rangées 3,12,5,6.
De cette manière, via l’apparition des blocs de taille irrégulière, l’analyse statistique directe n’est pas applicable. Ensuite, si nous voulons un codage plus efficace en termes de coût, il suffit de considérer des hypergroupes particuliers comme ceux qui ont un grand nombre d’éléments projectifs.
