3351 - L’apport de Weierstrass en calcul fonctionnel selon Carathéodory
N. Lygeros
Dans le cadre de son analyse de l’ouvrage de Jacques Hadamard intitulé Leçons sur le calcul des variations, Carathéodory est amené à mettre en avant l’apport de Weierstrass en calcul fonctionnel. Sa première remarque a trait à la notion de voisinage de deux surfaces définies par des ensembles de fonction. En effet pour des fonctions ordinaires, la notion de voisinage est élémentaire car elle comporte un élément statique. Tandis que le voisinage dans le calcul fonctionnel doit tenir compte d’un aspect dynamique inhérent aux fonctions. C’est pour cette raison que nous sommes obligés de distinguer divers ordres de voisinage à l’instar de Zermelo qui a développé et étudié les idées de Weierstrass. L’apport de ce dernier est encore plus clair lorsque nous étudions le problème du calcul des variations mais surtout les problèmes sous forme paramétrique. La base de ces recherches s’appuient sur les premières fonctionnelles pour lesquelles Bernoulli, Euler et Lagrange ont résolu le problème du calcul des variations lorsqu’elles ont toutes la forme particulière d’une intégrale définie
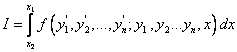
où y1, y2,…yn sont des fonctions inconnues de x dont l’ensemble représente une courbe de l’espace à n+1 dimensions. Weierstrass est le premier a avoir reconnu l’importance des problèmes paramétriques pour généraliser ce type de résultat. Cette approche est somme toute naturelle si nous examinons le point de vue que nous avons étudié dans une précédente note sur la définition d’une fonctionnelle et ses conséquences sur le champ fonctionnel. Cependant Weierstrass est allé encore plus loin et dans ses cours, il n’a traité presque que celles-ci. Aussi il surmontait une difficulté intrinsèque des courbes. En effet certains des problèmes du calcul des variations qui ont une signification géométrique ne peuvent être ramenés à des fonctions sans l’utilisation des paramètres. Il faudrait pour cela sectionner la courbe en morceaux afin de la transformer en fonction ordinaire. Seulement ce procédé n’est pas uniquement artificiel, il est parfois impossible car il présuppose une connaissance de la courbe, ce qui n’est pas toujours le cas. Les problèmes paramétriques avaient été traités avant Weierstrass, et Carathéodory cite les exemples de l’action maupertuisienne et la théorie des rayons lumineux d’Hamilton. Néanmoins, Weierstrass a systématisé cette approche. Un autre point sur lequel l’apport de Weierstrass est essentiel se trouve dans les conditions suffisantes. Le problème est le suivant: trouver la courbe joignant deux points pour laquelle la fonctionnelle I a la plus petite valeur possible. Si la solution existe alors elle est nécessairement extrémale. Mais ce problème n’a pas toujours une solution. Weierstrass via l’introduction de ses fonctions E a donné une méthode qui permet la comparaison de la valeur d’une intégrale I prise le long d’une courbe quelconque dans un champ -courbe de comparaison – et la valeur I de cette intégrale prise le long d’une extrémale ayant les mêmes extrémités. Toujours selon Carathéodory la méthode de Weierstrass consiste à représenter la différence J-I par une intégrale curviligne sur la fonction E. Aussi si nous pouvons assurer la possibilité de cette fonction E pour toutes les courbes du champ, la grandeur J-I aura aussi cette propriété. Ainsi I sera inférieur à J et la propriété de minimum sera démontrée. D’où l’importance de la fonction E de Weierstrass.
