2565 - Réflexions sur les intervalles de Bruhat des groupes de Coxeter
N. Lygeros
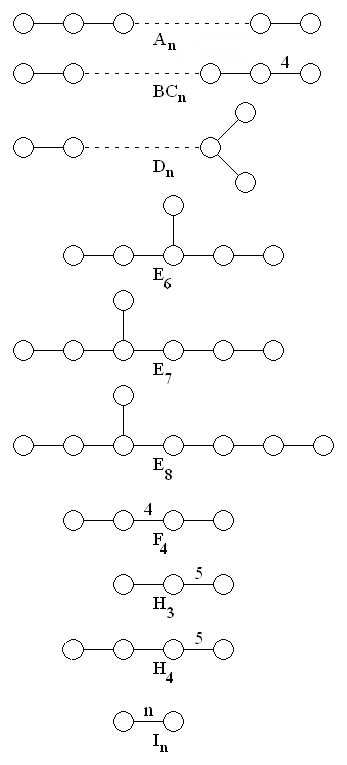
Les groupes de réflexions complexes sont des groupes finis de matrices à coefficients dans une extension abélienne finie du corps des rationnels, engendrés par des pseudo-réflexions. Si le corps des coefficients est réel alors nous avons les groupes de Coxeter. Quant aux groupes de Weyl, ce sont les groupes finis de matrices à coefficients dans le corps des rationnels, engendrés par des réflexions. Des cas particulièrement classiques de groupes de Coxeter sont les groupes diédraux i.e. groupes de symétries d’un polygone régulier, et les groupes d’isométries de polyèdres réguliers.
Notre approche des groupes de Coxeter et en particulier des ordres de Bruhat, nous a été suggérée par Fokko du Cloux à la suite de la lecture des travaux de Matthew Dyer. L’importance de l’ordre de Bruhat sur un groupe de Coxeter provient entre autres du fait qu’il décrit les motifs des cellules de Schubert pour les groupes algébriques réductibles sur des corps algébriquement clos mais aussi les inclusions sur les modules de Verma pour une algèbre de Lie semi-simple complexe. Fokko du Cloux nous a fait observer que Matthew Dyer avait résolu la question de Bjorner et ainsi démontré qu’il n’existe à isomorphie près qu’un nombre fini de posets qui soient des intervalles de Bruhat dans les groupes de Coxeter finis. L’intérêt de ce type d’approche provient du fait que le polynôme de Kazhdan-Lusztig Px,y semble ne dépendre que du type d’isomorphisme de l’intervalle de Bruhat [x,y]. Cette conjecture permettrait d’améliorer encore plus l’implémentation du programme Coxeter de Fokko du Cloux. Matthew Dyer ne s’est pas contenté d’énoncer un résultat théorique, il a aussi étudié des cas spécifiques. Il a obtenu des classes de posets qui apparaissent comme intervalles dans l’ordre de Bruhat. Par exemple il a montré qu’un intervalle de Bruhat avec exactement deux atomes (ou coatomes) est isomorphe à un intervalle de Bruhat du groupe diédral. C’est ainsi que nous avons décidé avec Fokko du Cloux d’étudier la structure explicite des intervalles de Bruhat de certains groupes de Coxeter finis. Pour cela il a modifié les sorties de son programme Coxeter afin que nous puissions les exploiter à l’aide d’une version modifiée de notre programme sur l’énumération des posets à isomorphie. Nous avons ensemble dépassé les difficultés techniques de cette approche, fait qui nous a permis d’avoir un outil puissant pour classifier les intervalles de longueur quatre du groupe de Coxeter F4. Le résultat de notre classification est illustré sur la figure suivante :

Nous avons utilisé le formalisme des graphes mineurs et mis en évidence de manière explicite et effective que la conjecture de Dyer sur la représentabilité des intervalles de Bruhat en tant que « triangulation » de la sphère est correcte pour tous les intervalles de Bruhat de longueur quatre du groupe de Coxeter fini F4.
Par la suite Fokko du Cloux s’est inspiré de ces travaux et en particulier du traitement des nombres de Betti en tant que couche des posets associés, pour améliorer les ressources de son programme Coxeter. Nous espérons avoir ainsi contribué à notre manière à ce que cette invention de Fokko du Cloux dépasse le cadre étroit de sa vie et continue à aider les mathématiciens à étudier les groupes de Coxeter qu’il aimait tant.