2165 - Sur la fonction rationnelle de C. Carathéodory et L. Féjer
N. Lygeros
L’historique de la découverte de la fonction rationnelle de C. Carathéodory et L. Féjer, débute avec la publication de l’article de J. Jensen intitulé Sur un nouvel et important théorème de la théorie des fonctions paru dans Acta mathematica, tome XXII, p. 357-364, en 1899. Dans cet article, grâce à des considérations sur le potentiel logarithmique, J. Jensen parvient à trouver une solution implicite au problème suivant.
Problème : Quelle est parmi toutes les fonctions de variable complexe f (z), holomorphes à l’intérieur du cercle ![]() , prenant pour z = 0 la valeur donnée A et s’annulant aux points
, prenant pour z = 0 la valeur donnée A et s’annulant aux points ![]() , celle dont le maximum M de la valeur absolue à l’intérieur du cercle est le plus petit possible ?
, celle dont le maximum M de la valeur absolue à l’intérieur du cercle est le plus petit possible ?
Dans le cadre établi par le résultat de J. Jensen, il n’existe pas de fonction explicite. Alors que la recherche de C. Carathéodory et L. Féjer adopte un autre point de vue. Celui-ci est élémentaire quant à sa méthodologie et efficace quant au résultat.
En utilisant les points conjugués de ![]() par rapport au cercle
par rapport au cercle ![]() , ils forment l’expression
, ils forment l’expression
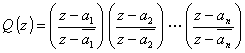
Pour chaque fonction solution du problème, on peut écrire : ![]() .
.
Q (z) est également holomorphe à l’intérieur du cercle et de plus :
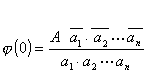 or
or  donc
donc 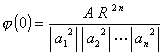
Comme la valeur absolue de Q (z) est constante sur le cercle ![]() , ils écrivent
, ils écrivent
![]()
Ainsi ![]()
or 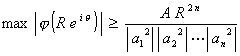
Ils obtiennent de cette manière élémentaire l’inégalité de J. Jensen à savoir :
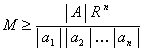
Cependant ils ont de plus la solution explicite du problème initial :
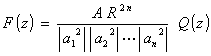
C’est cette solution que nous appellerons désormais la fonction rationnelle de Carathéodory et Féjer. Ils remarquent enfin dans leur article que cette valeur M est optimale même si les fonctions régulières sont remplacées par des fonctions entières. De cette manière, Carathéodory et Féjer ont, via l’élémentarité de leur démonstration, précisé la véritable complexité du problème en dehors de l’appareil technique du potentiel logarithmique.
