2008 - Η συμβολή του δυνητικού
N. Lygeros
Όταν εξετάζουμε το θέμα της θεμελιακής απροσδιοριστίας του Heisenberg, δεν κοιτάζουμε τις προεκτάσεις στην κβαντική μηχανική. Αυτή η αρχή παράγει αποτελέσματα που είναι τόσο βασικά και τόσο ριζοσπαστικά που δεν κατανοούμε κατά πόσο αντικρούουν την κοινή λογική, η οποία δεν έχει σχέση με τη λογική. Η αρχή της κβαντικής μηχανικής είναι με άλλα λόγια και ένα πρόβλημα μη επιλογής. Όχι επειδή δεν υπάρχει επιλογή, αλλά διότι δεν έχει νόημα. Η ίδια η έννοια της διασταύρωσης δεν έχει νόημα όταν τα σωματίδια είναι τα ίδια. Στην ερώτηση
 ή
ή 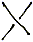 , η κβαντική μηχανική απαντά
, η κβαντική μηχανική απαντά 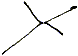 και
και 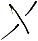 . Δηλαδή μετατρέπει την επιλογή ή μάλλον τη μη επιλογή σε σύνθεση. Όμως δεν δίνουμε τόσο μεγάλη σημασία στη μεταμόρφωση του Η σε ΚΑΙ. Αν το εξετάσουμε πιο βαθιά το θέμα με τις β-διασπάσεις, τότε ανακαλύπτουμε και τη συμβολή του δυνητικού. Στις δυνητικές διαδικασίες δεν εμφανίζονται παρατηρήσιμα μποζόνια. Όταν όμως μελετάμε τη διάσπαση του μιονίου, τα μποζόνια παίζουν τον ρόλο του μεσάζοντα. Συνεπώς, υπάρχει μια πληροφορία που μεταφέρεται μέσω του πεδίου. Ενώ έχουμε:
. Δηλαδή μετατρέπει την επιλογή ή μάλλον τη μη επιλογή σε σύνθεση. Όμως δεν δίνουμε τόσο μεγάλη σημασία στη μεταμόρφωση του Η σε ΚΑΙ. Αν το εξετάσουμε πιο βαθιά το θέμα με τις β-διασπάσεις, τότε ανακαλύπτουμε και τη συμβολή του δυνητικού. Στις δυνητικές διαδικασίες δεν εμφανίζονται παρατηρήσιμα μποζόνια. Όταν όμως μελετάμε τη διάσπαση του μιονίου, τα μποζόνια παίζουν τον ρόλο του μεσάζοντα. Συνεπώς, υπάρχει μια πληροφορία που μεταφέρεται μέσω του πεδίου. Ενώ έχουμε:
μ– → νμ + e– + νe, τα διαγράμματα του Feynman είναι τα εξής:
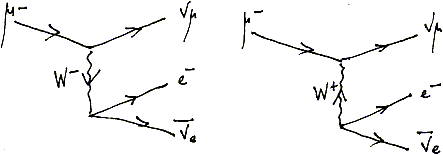
Στο πρώτο διάγραμμα, το μπόζονιο W– διασπάται σε ηλεκτρόνιο και αντινετρίνο του ηλεκτρονίου. Ενώ στο δεύτερο διάγραμμα, το μποζόνιο W+ δημιουργείται από το κενό. Και στις δύο περιπτώσεις τα μποζόνια είναι δυνητικά. Όμως είναι ακριβώς αυτή η δυνητική τους οντότητα που εξηγεί τη διάσπαση του μιονίου. Και μάλιστα δίνει και μια ερμηνεία για την παραβίαση της ομοτιμίας, η οποία δεν είναι δυνητική αλλά πραγματική. Η συμμετρία των μποζονίων W+ και W– δεν επιτρέπει να επιλέξουμε μεταξύ των δύο διαγραμμάτων του Feynman. Αλλά σε κάθε περίπτωση έχουμε παραβίαση. Η μη επιλογή έχει και αυτή ιδιότητες, οι οποίες πρέπει να είναι αποτελεσματικές για να αποδείξουμε πρακτικά αποτελέσματα, όπως μια καλύτερη κατανόηση της έννοιας της στροφορμής, το λεγόμενο σπιν. Πιο θεωρητικά ακόμα ανακαλύπτουμε και την αναγκαιότητα του εργαλείου του τανυστή διότι το διάνυσμα δεν αντέχει φαινόμενα όπως η β-διάσπαση ή πιο απλά ακόμα η εμφάνιση του μαγνητικού πεδίου. Κατά συνέπεια, το δυνητικό στοιχείο είναι ένα ευρηματικό εργαλείο για την επινόηση εξηγήσεων μεγαλύτερης κατανόησης ενός φαινομένου. Ακολουθούν τα νοητικά σχήματα που παράγει η εισαγωγή μιγαδικών αριθμών στα μαθηματικά. Μέσω της ύπαρξής τους, δίνουν πρόσβαση σε πραγματικότητες που θα παρέμεναν άπιαστες, αν περιορίζαμε τη μελέτη μας σε πραγματικά εργαλεία. Διότι το δυνητικό έχει περισσότερους βαθμούς ελευθερίας από την πραγματικότητα.
