Dans le cadre de l’enseignement de la logique, il existe une difficulté due à l’aspect lexical du calcul propositionnel mais aussi de cadres plus complexes. Aussi restreindre l’apprentissage de la logique à un jeu formel d’écriture serait une erreur non seulement cognitive mais aussi mathématique. Un exemple concret des possibilités offertes par la logique et son interprétation cognitive est représentée par l’apport du philosophe John Venn. Celui-ci a créé ce que nous nommons désormais les diagrammes de Venn. Ces fameux diagrammes permettent de visualiser de manière efficace les propositions logiques. Conscient de la nécessité d’une représentation non verbale pour appréhender grâce à ses travaux, The logic of Chance, Symbolic Logic, The Principles of Empirical and Inductive Logic. Les diagrammes de Venn peuvent eux-mêmes êtres considérés comme une combinaison de la théorie des ensembles et de l’algèbre de Boole. L’idée de cette visualisation, c’est de montrer d’une part les contre-exemples possibles d’une proposition et d’autre part la visualisation de propositions.

Contre-exemple:

∀x ∈A : x ∈B

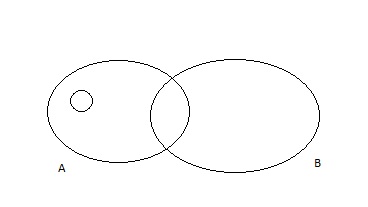
Le centre est représenté par O.

Exemple : ∀x ∈A : x ∈B

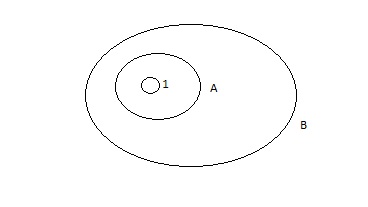
La validation est représentée par 1.

En réalité, cette représentation ensembliste permet de traiter très rapidement les syllogismes logiques mais aussi certaines erreurs si présentes dans les livres de philosophie. Car les syllogismes se représentent par un triplet de cercles. De cette manière il est possible de mieux comprendre la problématique de la causalité via la généralisation de la représentation par inclusion de cercles et encore plus généralement par inclusion d’hypersphères. Ainsi un outil visuel permet non seulement de généraliser un problème de logique mais aussi d’ouvrir une voie pour accéder à des résultats via la géométrie. Réciproquement ce lien entre la géométrie et la logique rend possible la codification formelle de problèmes géométriques. Il n’est donc pas surprenant que du point de vue didactique, cette approche géométrique active efficacement la vision de l’étudiant dans un domaine où il est nécessaire d’aborder de manière multiple de problèmes. Cela permet aussi d’aider des étudiants qui ont des difficultés d’ordre linguistique puisque la géométrie leur donne la possibilité de compenser et de surmonter cognitivement ce handicap. Aussi l’enseignant dispose d’un champ plus vaste pour présenter la logique.