1599 - Interprétation géométrique de la dérivée d’une fonction réelle
N. Lygeros
Une des principales difficultés de la compréhension de la nature de la dérivée d’une fonction réelle provient de l’aspect géométrique. Nous observons cette difficulté auprès des étudiants qui préfèrent naturellement regarder la dérivation comme un simple opérateur sans nécessairement l’associer à une représentation graphique. Le problème de cette approche c’est qu’elle élimine de facto tout aspect dynamique de la dérivée puisque celle-ci n’est plus considérée comme une limite. Ceci est d’autant plus grave que c’est bien souvent associé à une mauvaise notation. En effet, même les étudiants ont du mal à se rendre compte que la notation : f ‘ (x0) est nécessairement égale à zéro. Car la dérivation et la stabilisation ne sont pas commutantes. C’est pour cela qu’il est nécessaire d’écrire ![]() lorsque nous voulons considérer la valeur de la dérivée au point x0.
lorsque nous voulons considérer la valeur de la dérivée au point x0.
Pour comprendre vraiment la nature de la dérivée qui n’a de sens que si la fonction est continue, nous devons revenir à l’aspect dynamique de la limite.
![]()
Aussi il est nécessaire de parler du coefficient directeur, de la pente de la trajectoire en ce point. Il ne s’agit pas d’apposer un point de vue mécanique à cette entité et ce, de manière artificielle. Mais bien de visualiser concrètement le déplacement du point mobile sur la courbe et de lui associer une droite qui passe par lui-même et le point de coordonnées ![]() . Dans l’esprit des étudiants ce processus doit être mobile comme nous pouvons le visualiser ici.
. Dans l’esprit des étudiants ce processus doit être mobile comme nous pouvons le visualiser ici.
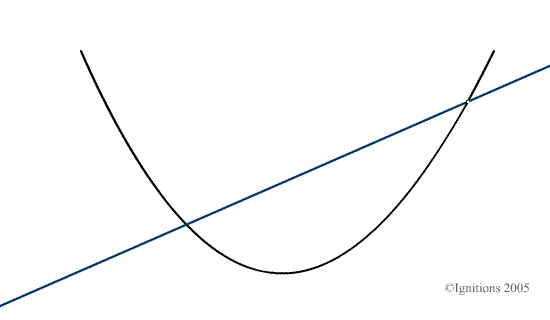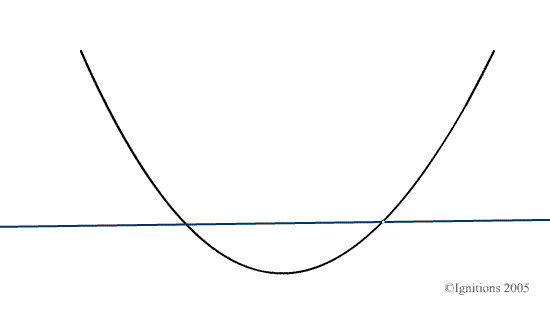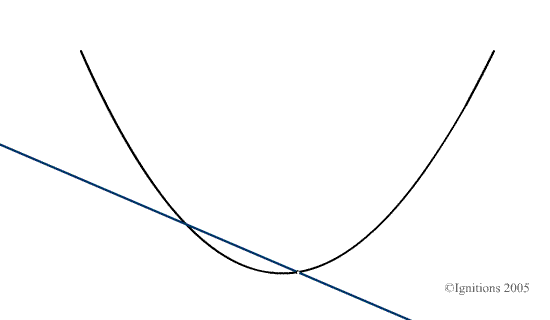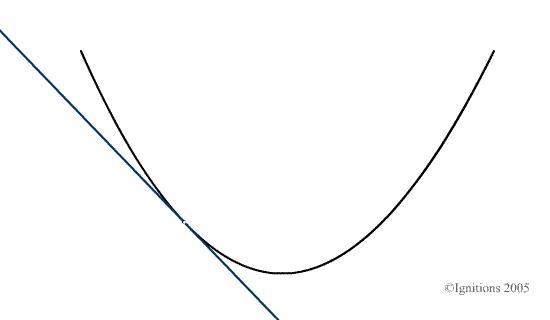
De cette manière, la dérivée n’est plus simplement une entité statique mais bien le résultat d’un passage à la limite et donc d’un processus qui évolue. C’est ce schéma mental dynamique qui doit représenter la dérivée, si nous voulons vraiment que les étudiants puissent effectuer le passage géométrique nécessaire qui leur permettra par la suite de comprendre la dérivation dans le monde complexe puis les notions de variété, de métrique et de carte. Dans ce cadre, la dérivée d’une fraction réelle ne représente qu’une étape à franchir certes, mais seulement une étape. La considérer de manière statique comme une fin en soi est une grave erreur du point de vue didactique qui est immédiatement sensible dès l’approche du calcul différentiel et plus encore du calcul intégral.
Il ne faudrait pas pour autant confondre la pente avec la tangente mais cette difficulté n’est qu’artificielle. Par contre, il faudrait être plus vigilant pour la visualisation de la notion de point d’inflexion et exploiter celle de rayon de courbure et de changement de courbure. Ce point nécessite tout un travail autour de la notion de convexité qui peut se prolonger sur celle de l’enveloppe convexe.
