1080 - Remarques sur les matrices singulières d’ordre deux
N. Lygeros
Considérons l’ensemble des matrices singulières d’ordre deux à savoir les matrices de la forme ![]() qui multipliées à droite ou à gauche avec des matrices de la même forme donnent la matrice nulle. Plus formellement :
qui multipliées à droite ou à gauche avec des matrices de la même forme donnent la matrice nulle. Plus formellement :
![]()
Aussi si ![]() alors
alors ![]() comme
comme ![]()
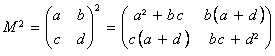
Supposons que ![]() et
et ![]() alors
alors ![]() .
.
Donc M est nécessairement de la forme ![]() avec
avec ![]() .
.
Aussi 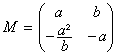 .
.
Considérons la matrice G telle que ![]() :
: 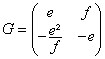 .
.
Comme 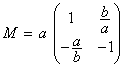 et
et 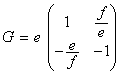
en enlevant la partie scalaire nous avons
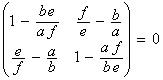
et ceci est équivalent à ![]()
or cette condition équivaut elle-même à ![]() .
.
Cela prouve que nous ne pouvons avoir deux paramètres libres.
Ainsi M est nécessairement de la forme : ![]() ou encore
ou encore ![]()
et comme 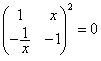 la condition est aussi suffisante.
la condition est aussi suffisante.
Par conséquent : ![]() . □
. □
